ベイズの定理でモンティ・ホール問題に挑戦！

確率においてよく知られているモンティ・ホール問題は、論理的思考とベイズの定理の応用を組み合わせることによって解くことができます。この記事では、ベイズの定理を用いてモンティ・ホール問題を分析し、論理的な決定を下す方法について説明します。

ベイズの定理でモンティ・ホール問題に挑戦！

ベイズの定理でモンティ・ホール問題に挑戦！

モンティ・ホール問題とは？

モンティ・ホール問題は、1960年代にアメリカのゲーム番組「Let's Make a Deal」の司会者であるモンティ・ホールが考案したことから名付けられた確率の問題です。この問題は、直感的には理解しにくい解答が導かれることで有名です。

問題の内容

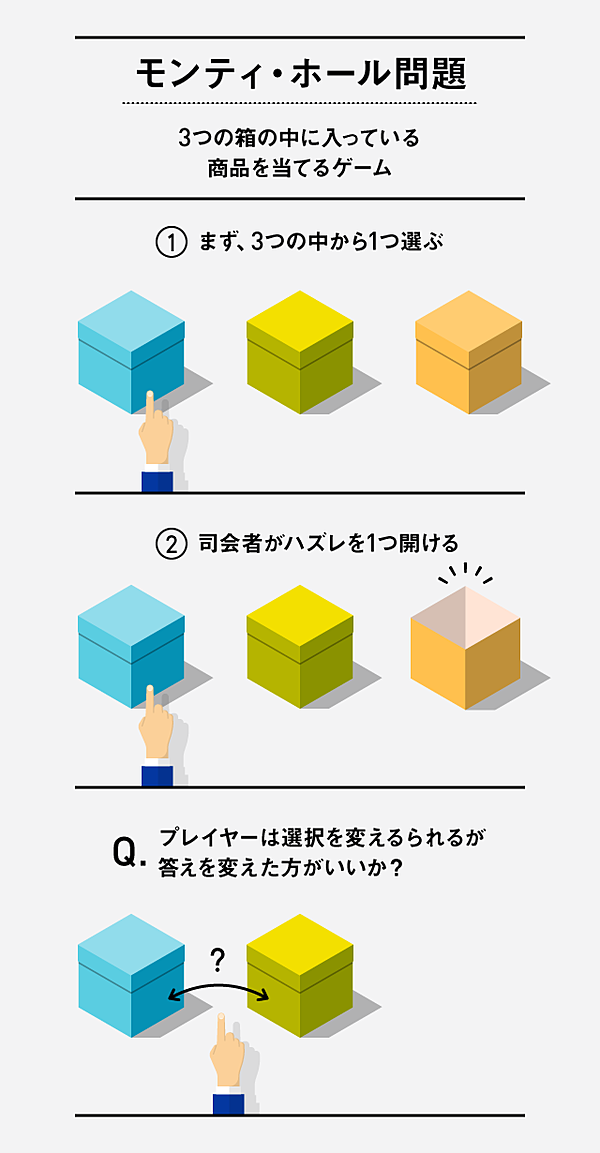
プレイヤーは、3つのドアの中から1つを選択し、その裏に隠されている賞品を獲得しようとします。3つのドアのうち、1つのドアの裏には賞品（例えば、車）があり、残りの2つのドアの裏にははずれ（例えば、ヤギ）が隠されています。

プレイヤーがドアを選択した後、司会者は残りの2つのドアのうち、はずれが隠されているドアを1つ開けてプレイヤーに見せます。そして、プレイヤーに「選択したドアを変更しますか？」と質問します。

この時、プレイヤーは選択したドアを変更すべきでしょうか、それとも変更せずにそのままにするべきでしょうか？

ベイズの定理との関係

ベイズの定理は、事前の情報（事前確率）と新しい情報（尤度）を組み合わせて、事後の確率を計算する定理です。モンティ・ホール問題では、プレイヤーが最初にドアを選択した後、司会者がドアを開けるという新しい情報が得られます。この新しい情報を利用して、プレイヤーが最初に選択したドアに賞品がある確率を再計算することで、最適な戦略を導き出すことができます。

ベイズの定理による分析

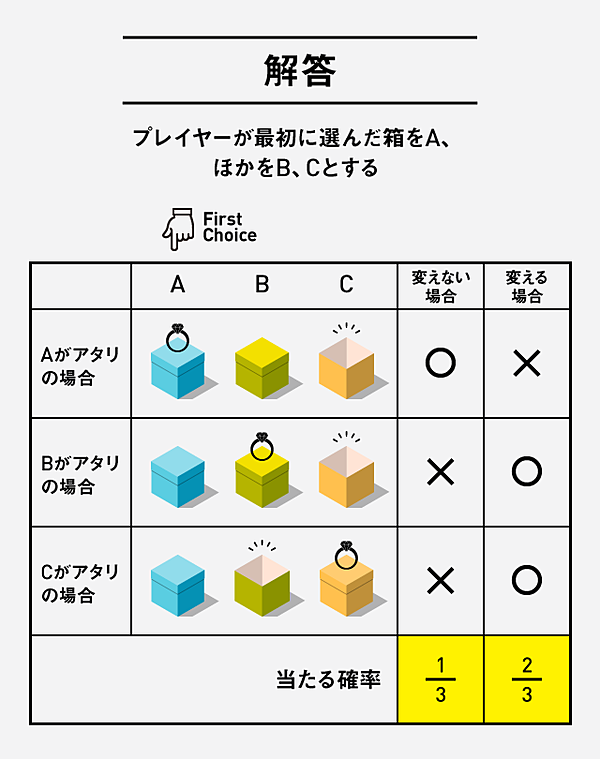
1. 事前確率: プレイヤーが最初にドアを選択した時、そのドアに賞品がある確率は1/3です。
2. 尤度: 司会者がドアを開けて、はずれが隠されているドアを見せた時、プレイヤーが最初に選択したドアに賞品がある場合、司会者は残りの2つのドアから必ずはずれが隠されているドアを開けることができます。一方、プレイヤーが最初に選択したドアにはずれがある場合、司会者は残りの2つのドアから賞品が隠されているドアを開ける必要があります。
3. 事後確率: ベイズの定理を用いて、これらの事前確率と尤度を組み合わせることで、プレイヤーが最初に選択したドアに賞品がある確率を再計算できます。

モンティ・ホール問題の解答

ベイズの定理を用いた分析の結果、プレイヤーが最初に選択したドアを変更する方が、賞品を獲得する確率が高くなることがわかります。

具体的には、最初に選択したドアを変更した場合、賞品を獲得する確率は2/3となり、変更しない場合は1/3となります。

モンティ・ホール問題の結論

モンティ・ホール問題は、直感的に理解しにくい問題ですが、ベイズの定理を用いることで、合理的かつ最適な解答を導き出すことができます。

モンティ・ホール問題の元ネタは？

モンティ・ホール問題の元ネタ

モンティ・ホール問題は、1963年にアメリカのゲーム番組「Let's Make a Deal」で司会を務めていたモンティ・ホールからその名前が付けられました。番組のルールは、3つのドアの中から賞品が入っているドアを選び、その後、司会者が残りの2つのドアのうち、賞品がないドアを開けてから、最初の選択を変更するかどうかをプレイヤーに尋ねるというものでした。

モンティ・ホール問題の起源

モンティ・ホール問題は、数学者マーティン・ガードナーが1990年に雑誌「サイエンティフィック・アメリカン」に掲載したコラムで紹介されたことで広く知られるようになりました。ガードナーは、この問題を「三囚人問題」と呼び、確率論における一見直感に反する結果について議論していました。

モンティ・ホール問題の数学的背景

モンティ・ホール問題は、条件付き確率という概念に基づいています。つまり、ある情報を得た後に、ある事象が起こる確率が変化するというものです。モンティ・ホール問題では、司会者が賞品がないドアを開けるという情報が得られたことで、最初の選択を変更すると、賞品を獲得する確率が2倍になることが数学的に証明されています。

モンティ・ホール問題の誤解

モンティ・ホール問題は、多くの誤解を生み出しています。最も一般的な誤解の一つは、司会者が賞品がないドアを開けることで、残りのドアの確率が50%ずつになるという考え方です。しかし、司会者が事前に賞品の場所を知っているため、残りのドアの確率は異なるのです。

モンティ・ホール問題の教訓

モンティ・ホール問題は、直感に反する確率の問題であることを示しています。この問題は、私たちがどのように確率を理解しているのか、そして直感的な判断が常に正しいとは限らないことを教えてくれます。

モンティ・ホール問題のルールは？

モンティ・ホール問題とは

モンティ・ホール問題は、確率論と直感的な思考のギャップを浮き彫りにする有名な思考実験です。この問題は、アメリカ合衆国のテレビ番組「Let's Make a Deal」の司会者であったモンティ・ホールにちなんで名付けられました。

問題のルール

モンティ・ホール問題は、次のようなルールで展開されます。

1. 3つのドアがあり、そのうちの1つのドアの後ろには賞品（例えば、車）があり、他の2つのドアの後ろにはヤギがあります。
2. あなたは賞品のあるドアを選択する必要があります。
3. あなたを選択した後、司会者はあなたが選ばなかった残りの2つのドアのうち、必ずヤギがいるドアを1つ開けます。
4. その後、司会者はあなたに、「最初に選択したドアを選び続けるか、残りの閉まっているドアに切り替えるか」と尋ねます。

なぜドアを切り替えるのが有利なのか

この問題の直感的な答えは、ドアを切り替えても変わらないということです。なぜなら、残りの2つのドアのどちらか一方に賞品がある確率は50%だからです。しかし、実際にはドアを切り替えることで賞品を獲得する確率が2倍になります。

ドアを切り替えることの利点

ドアを切り替えることで、賞品を獲得する確率が2倍になる理由は、次のとおりです。

1. 最初に選択したドアが賞品のあるドアである確率は1/3です。
2. 最初に選択したドアがヤギのあるドアである確率は2/3です。
3. 司会者がヤギのあるドアを開けた後、残りの閉まっているドアには、最初の選択がヤギのあるドアであった場合の確率（2/3）が集中します。

モンティ・ホール問題の教訓

モンティ・ホール問題は、確率論では直感的な思考が必ずしも正しいとは限らないことを示しています。問題を正しく理解し、すべての可能性を考慮することが重要です。

モンティ・ホール問題で100個開ける確率は？

モンティ・ホール問題で100個開ける確率は、実際には 0% です。なぜなら、この問題は100個のドアではなく、3つのドア を前提としているからです。

モンティ・ホール問題の概要

モンティ・ホール問題は、確率論における有名な思考実験です。この問題では、プレイヤーは3つのドアから1つを選択し、その裏に賞品が隠されています。プレイヤーがドアを選んだ後、司会者は残りの2つのドアのうち、賞品がないドアを1つ開けて、プレイヤーに別のドアを選ぶか、最初の選択を維持するかを尋ねます。

モンティ・ホール問題の解法

モンティ・ホール問題の解法は、次のように説明できます。

プレイヤーは最初に3つのドアから1つを選びます。この時点で、そのドアに賞品がある確率は1/3です。
司会者は、残りの2つのドアのうち、賞品がないドアを1つ開けます。これは、プレイヤーの最初の選択に影響を与えません。
プレイヤーは、最初の選択を維持するか、別のドアを選ぶことができます。別のドアを選ぶ場合、そのドアに賞品がある確率は2/3になります。これは、司会者が賞品がないドアを開けたことで、残りのドアの確率が集中したためです。

モンティ・ホール問題の誤解

モンティ・ホール問題を理解する上で、よくある誤解は、司会者がドアを開けることで、残りの2つのドアの確率が50%ずつになるということです。しかし、これは誤りです。司会者は、賞品がないドアを意図的に開けるため、プレイヤーの最初の選択に影響を与える情報を与えています。

モンティ・ホール問題の結論

モンティ・ホール問題は、確率論における直感に反する結果を示す例です。この問題は、私たちが確率をどのように理解し、どのように意思決定を行うかを教えてくれます。

モンティ・ホール問題の確率はなぜ変わるのですか？

モンティ・ホール問題の確率が変わる理由

モンティ・ホール問題は、一見確率が変わらないように思えるのに、実は選択を変更することで勝率が大幅に上昇する、直感に反する問題として知られています。この確率の変化は、モンティがドアを開けて「はずれ」のドアを明らかにするという追加情報によって生じます。ここでは、なぜ確率が変わるのか、その理由を詳しく解説していきます。

初期選択の確率

はじめに、あなたは3つのドアの中から1つを選びます。この時点では、あなたが選んだドアの後ろに当たりがある確率は1/3、残りの2つのドアの後ろに当たりがある確率は2/3です。

1. あなたが選んだドアの後ろに当たりがある確率は、初期段階では1/3です。
2. 残りの2つのドアの後ろに当たりがある確率は、初期段階では2/3です。

モンティの行動による情報の提供

モンティは、あなたが選んだドア以外の2つのドアのうち、必ずはずれのドアを開けます。この行為によって、重要な情報が提供されます。モンティがドアを開けることで、残りのドアの当たりである確率が集約されます。つまり、あなたが選んだドアがはずれのとき、残りのもう1つのドアは必ず当たりになります。

1. モンティは必ずはずれのドアを開けます。
2. モンティの行動によって、残りのドアの当たりである確率が集中します。

選択変更による確率の変化

あなたが最初に選んだドアがはずれのとき、モンティがドアを開けることで、残りのドアは必ず当たりになります。そのため、選択を変更することで、勝率が2/3になります。逆に、あなたが最初に選んだドアが当たりのとき、選択を変更すると、必ずはずれになります。しかし、最初に選んだドアが当たる確率は1/3なので、選択を変更しても、勝率は1/3のままです。

1. 最初に選んだドアがはずれのとき、選択を変更すると必ず当たります。
2. 最初に選んだドアが当たりのとき、選択を変更すると必ずはずれます。

確率の計算

モンティ・ホール問題では、選択変更による確率の変化を、条件付き確率を用いて計算することができます。条件付き確率とは、ある事象が起きたときに、別の事象が起きる確率のことです。この問題では、モンティがドアを開けたという情報が、あなたの選択を変更する確率に影響を与えます。

1. モンティ・ホール問題は条件付き確率で説明できます。
2. モンティの行動は、あなたの選択の確率に影響を与えます。

まとめ

モンティ・ホール問題の確率が変わるのは、モンティがドアを開けて情報を提供することで、残りのドアの当たりである確率が集中し、選択変更による勝率が2/3になるからです。

詳細情報

モンティ・ホール問題ってそもそも何ですか？

モンティ・ホール問題は、アメリカのゲームショー「Let's Make a Deal」の司会者、モンティ・ホールの名前から名付けられた確率論の問題です。
この問題は、3つのドアがあり、そのうちの1つにのみ賞品が隠されているという設定です。
あなたは1つのドアを選択し、選択したドアの後ろに賞品があるかどうかが分かります。
しかし、その前に、司会者はあなたが選択していない残りの2つのドアのうち、賞品がないドアを必ず1つ開けます。
そして、あなたは自分の最初の選択を変更するか、それとも最初の選択を維持するかを選ぶことができます。
この問題では、選択を変更する方が賞品を獲得する確率が高くなるという意外な結論が導き出されます。

ベイズの定理ってモンティ・ホール問題にどう役立つんですか？

ベイズの定理は、事前の確率と新たな情報に基づいて事後の確率を更新するのに役立つ強力なツールです。
モンティ・ホール問題では、ベイズの定理を使って、ドアを変更したときに賞品を獲得する確率を計算することができます。

初めに、あなたは3つのドアのいずれかに賞品がある確率が等しいと仮定します。
これは、事前確率と呼ばれます。

次に、司会者がドアを開けるという新たな情報が与えられます。
この情報によって、あなたの最初の選択が正しい確率と間違っている確率が変化します。

ベイズの定理を使うことで、事後確率、つまり司会者がドアを開けた後の、あなたの最初の選択が正しい確率を計算することができます。

結果として、ドアを変更した方が賞品を獲得する確率が高いという結論が得られます。

モンティ・ホール問題でドアを変更した方が良い理由を簡単に説明できますか？

ドアを変更した方が良い理由は、司会者がドアを開ける行為によって、残りのドアの確率が変化するからです。

初めに、あなたが選んだドアの後ろに賞品がある確率は1/3です。
しかし、司会者が賞品がないドアを開けることで、残りのドア（あなたが最初に選ばなかったドア）の確率は2/3に上昇します。

つまり、ドアを変更することで、賞品が2/3の確率で残りのドアの後ろにあることになるのです。

モンティ・ホール問題は、実際にはゲームショーよりも、確率やベイズ統計の理解を深めるための良い例ですね。

確かに、モンティ・ホール問題は、一見単純に見える問題ですが、実際には確率の理解を深めるための優れた例です。
この問題を通して、私たちは新たな情報がどのように確率を更新するか、そしてベイズの定理がどのように役立つのかを学ぶことができます。

また、モンティ・ホール問題は、直感と確率のギャップを示すものでもあります。
人々は、ドアを変更しても確率は変わらないと直感的に感じる場合がありますが、実際にはドアを変更した方が賞品を獲得する確率が2倍になるのです。

ベイズの定理でモンティ・ホール問題に挑戦！ に類似した他の記事を知りたい場合は、Gijutsu カテゴリにアクセスしてください。